Quick Start

In this quick-start, we'll implement the basic Susceptible-Infected-Recovered epidemiological model. This compartmental model is typically described by a system of deterministic, ordinary differential equations :

In the case of small populations, the continuous property of the state space can be a poor assumption, and we may prefer to simulate each individual in the population as separate entities. We'll phrase this model in the language of discrete-state stochastic processes, particularly that of continuous-time Markov chains.

The model file

scotch models are defined in JSON format. For the SIR model above, with time in days, it would look like this :

{
    "States" : [
        "S",
        "I",
        "R"
    ],

    "InitialConditions" : {
        "S" : 99,
        "I" : 1,
        "R" : 0
    },

    "Parameters" : {
        "r0" : "18",
        "gamma" : "1/14"
    },

    "Events" : [
        [
            "r0 * gamma * S * I / (S+I+R)",
            {
                "S" : -1,
                "I" : 1
            }
        ],
        [
            "gamma * I",
            {
                "I" : -1,
                "R" : 1
            }
        ]
    ]
}

You can download this file here.

Running the model

Let's boot up scotch and begin simulating the system.

import scotch

# Read in the scotch model file
model = scotch.model("sir.json")

This will return :

scotch model with 3 states, 2 parameters, and 2 events.

States :
S, initial condition = 99
I, initial condition = 1
R, initial condition = 0

Parameters :
r0 = 18
gamma = 1/14

Let's see what happens over the course of thirty days.

model.plot(30)

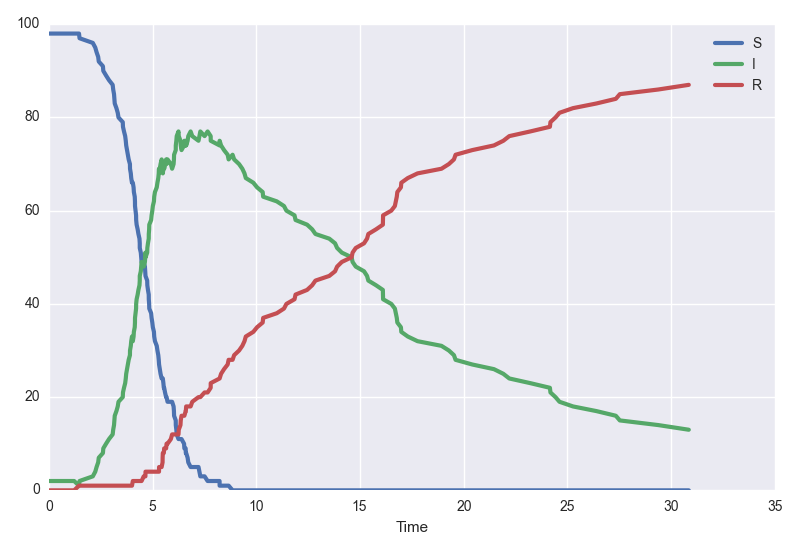
This is one realisation of the system. Perhaps we instead want to see average dynamics. Let's get the mean of one hundred trajectories and bootstrap some confidence intervals. We'll use the tau-leaping algorithm for speed.

model.plotsamples(30, algorithm="tauLeap", tau=0.25, trajectories=100, bootstrap=500)

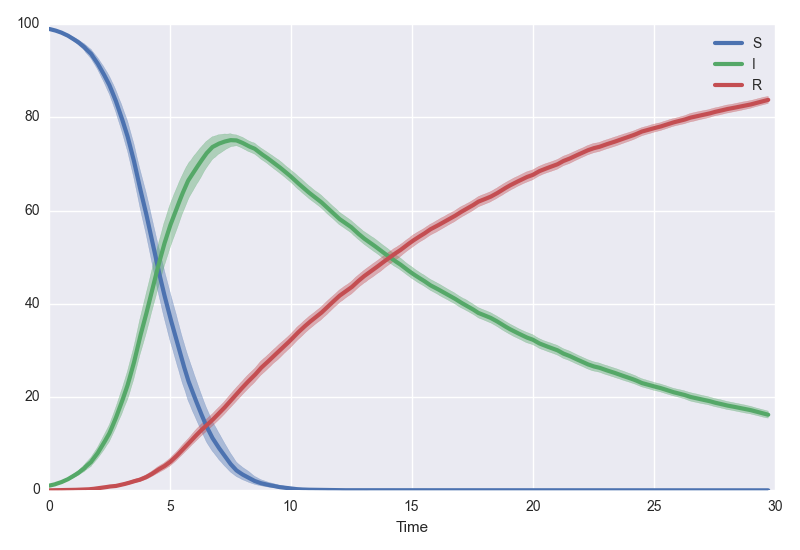
Both .plot and .plotsamples call .simulate under the hood. If you want scotch to return the traces of simulations to you, simply call

t, trace = model.simulate(30)

See the documentation for the complete API reference.